Files
der-1.gif
der-2.gif
dt-1.gif
dt-2.gif
dt-20.gif
dt-3.gif
dt-4.gif
fig-1.gif
index.html
lim-1.gif
MatlabPlotting.mp4
MatlabPlottingR2018a.mp4
newtons-method.gif
next_motif.gif
plt-8.gif
plts-1.gif
plts-2.gif
plts-3.gif
plts-4.gif
plts-5.gif
plts-6.gif
plts-7.gif
plts-7a.gif
previous_motif.gif
projectile-motion.mp4
projectile-motionR2018a.mp4
salary.mp4
salaryR2019a.mp4
shrt-1.gif
sin365.mp4
sin365R2018a.mp4
test.gif
tutorial-pieces.html
tutorial.html
tutorial001.gif
tutorial001.html
tutorial002.gif
tutorial002.html
tutorial003.gif
tutorial003.html
tutorial004.gif
tutorial004.html
tutorial005.gif
tutorial005.html
tutorial006.gif
tutorial006.html
tutorial007.gif
tutorial007.html
tutorial008.gif
tutorial008.html
tutorial009.gif
tutorial009.html
tutorial010.gif
tutorial010.html
tutorial011.gif
tutorial011.html
tutorial012.gif
tutorial012.html
tutorial013.gif
tutorial013.html
tutorial014.gif
tutorial014.html
tutorial015.gif
tutorial015.html
tutorial016.gif
tutorial017.gif
tutorial018.gif
tutorial019.gif
tutorial020.gif
tutorial021.gif
tutorial022.gif
zer-1.gif
zer-1a.gif
zer-2.gif
zer-3.gif
Using MATLAB in Calculus
Department of Mathematics, CSI
Last updated on
Welcome to the MATLAB tutorial.The intentions of this tutorial are:
- Be a guide to using MATLAB as a tool to study Calculus.
- Provide a quick way to get answers to MATLAB questions.
- Provide a collection of examples for your study of calculus and other math courses.
- Provide an archive of functions or m-files for your use.
- Be used as a starting point for web searches about MATLAB and mathematics. See the section on Resources .
- This tutorial is intended to be read on-line. This allows you to use the hypertext structure to move around the document with ease. You just point your mouse on a link and away you go. Use the back button on your browser to return to the previous screen. To orient yourself, there is a contents page and an index page .
- The contents page lists an outline of the tutorial. This is broken down by sections and subsections. This is useful if you know your topic and want to get there immediately.
- The index allows you to find references to a topic.
1 Other sources of help with MATLAB
If you are trying to find help with MATLAB you may want to try one of these:- On-line help is provided by the
help
command: For
example try this command to get help about the
plot
command:.
>> help plot
- You may find the web site of MATHWORKS
to be of help. Here you
will find
A collection of pre-written m-files .- information about the purchase of MATLAB.
- A technical notes FAQ (frequently asked questions).
- A list of books on MATLAB.
- other stuff...
2 Shortcuts
Included in this section are some tricks to make MATLAB easier to use.2.1 Windows stuff
The following shortcuts are for use with the Windows 3.1 version of MATLAB (version 4.2) that is installed in the computer labs. Newer versions may have different methods.- resizing the command window
To decrease the width of the MATLAB window, move the mouse pointer to the right border of the window. When the pointer is directly on the right border it will change to a double arrow. Press the left mouse clicker and while keeping it held down, move the mouse to the left. Notice that a highlighted line will appear denoting where the new right border will be. After you have re-positioned this vertical highlight about mid-screen, let go or the mouse clicker. Note that the MATLAB window is narrower, and that it is positioned on the left-hand side of the screen.
If you click on the upward-pointing arrow in the upper right hand corner of the MATLAB command window, the window will fill the whole screen and the button will turn into a double arrow. If you click on the double arrow, the window should return to its previous size.
- Moving the command window
Aim the mouse pointer at the title bar of the window. Then press the mouse left-hand clicker and, while keeping it pressed down, move the mouse, noting that a rectangular highlight moves along with it. This highlight tells us where the window will move to. Upon letting go of the mouse clicker, the window will be re-positioned there.
- Printing selected text
To print text from the command screen, you need first to select the text (mark a block of text). To do this, using the mouse, point to the beginning of the text. Press the left mouse button, and while holding down the button, move (drag) the pointer to the end of the text to be printed and then release the mouse button. You will see the selected text highlighted. Point to the ``FILE'' menu in the command window, click the left mouse button, and point to ``Print selected'' and click again. The selected text will be sent to the printer. (If this does not work, your computer may not be configured correctly---ask for help from a lab technician.) It is important that the desired text be first selected since, otherwise, the entire history of your MATLAB session will be printed---wasting a lot of paper!
- to print a graph from the figure window
To send your graph to the printer, click the mouse in the Figure Window. Then using the mouse, point the arrow to ``FILE" in the Figure Window and click the left mouse button. Then point the arrow to ``PRINT" and click again. Your figure will now be printed on the printer in the Computer Laboratory. WARNING: Make sure you are in the Figure Window -- if you are in the command window, MATLAB will print all your commands, from the start of the sessions.
- If the window you want is hidden, use Ctrl-Esc
(press the Ctrl key and Esc key at the same time). A box with a list of windows should appear. Click on the window you want, to select it, then click on ``switch to.''
- You can also use Alt-Tab:
pressing Tab repeatedly with the Alt key held down scrolls through the names of open windows. Release the Alt key when the window name you want appears. (These commands work in any Windows application.)
2.2 Command Line Editing
MATLAB has several tricks that will allow you to work faster when you work interactively.-
Using the Arrow keys
-
Moving to left and right along the line
The usual left and right arrow keys move you forward and backward along the line as you would expect.
- Exploring your command history
What is really convenient, is the use of the up and down arrows to scroll through your history. Hitting the up arrow puts the last command you entered in the command line. Hitting it twice will put the 2nd to last one. Guess what hitting it 3 times does? Did you go too far? Then the down arrow goes back down.
-
Moving to left and right along the line
- Moving along the line
MATLAB uses some keyboard shortcuts that are common in the UNIX world. In particular they come from the great editor emacs .-
Move to beginning of line
C-a: That's ``CONTROL - a'' pressed at the same time. The HOME key does the same. - Move to end of line
C-e: That's ``CONTROL - e'' pressed at the same time. The END key does the same - back one character
C-b: Same as left arrow. - forward one character
C-f: Same as right arrow. - ``kill'' all characters to the right
C-k: This will delete all the characters to the right of the cursor.
-
Move to beginning of line
-
The use of a ; can suppress the output:
Example:>> x = [1,2,3,4,5] % no semicolon ans = 1 2 3 4 5 >> x = [1,2,3,4,5]; % with a ``;'' there is no output
- several commands can be written on one line if separated
by semicolons (
;).
Example: The three lines>> x = linspace(0,6*pi); >> y = e.^(-x/10) * sin(x); % damped oscillation example >> plot(x,y);
could be one line>> x = linspace(0,6*pi);y = e.^(-x/10) * sin(x);plot(x,y);
3 How to work with numbers in MATLAB
To study Calculus using MATLAB we use a few features of MATLAB that allow us to store numbers, and lists of numbers.For a quick introduction click below, for a more thorough one, read on.
3.1 Quick introduction
A quick introduction to data typesWe make use of two types of data in using MATLAB for calculus: numbers, or scalars and lists or vectors. The words scalars and vectors are names given in a Linear Algebra course. How do we use these? Let's illustrate with an example:
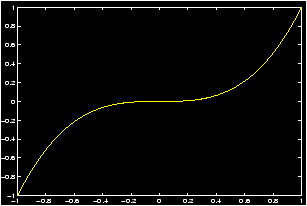
Example: sin2 x plot
Plot the function f(x) = sin2(p x) over the interval [0,2 p]. Answer:
What do we need to do to plot this?
If x was a number say 5, then we would compute f(5) in MATLAB in a manner similar to a what is done on a calculator:
>> sin( pi * 5 ) ^2 ans = 0However, we will use the plot command. Plotting is discussed in the section of plotting functions . To use the plot command, we need to generate a table of numbers for the x- and y- coordinates. Of course we would like to do this in the easiest way possible.
-
First generate a list of numbers for the x coordinates. One
way to do
this is with the
linspace
command.
>> x=linspace(0,2 * pi); % generates 100 numbers between 0 and 6.28...
To take a peak at what you have done type (its a mess)>> x % yikes 100 numbers!
- Next we generate the y values corresponding to the x
coordinates. So for each value in the list for x we need to
create the value of f(x). That is we multiply by p, then we
find the sine, then we square. Now we want to do this for all the
values in the list at once and here is where we need to be
careful. If x was just a number or
scalar
, say x=5, we
would simply type what we have above.
>> sin(pi*x)^2 % Won't work for out x!!
However, this won't work as x is a list of numbers. And we need to tell MATLAB to treat it the right way. So we do this in steps:-
multiply x by p. This is a number times a list. MATLAB does
this as you would expect
>> pi * x % multiplies each element of x by pi
- find the sine of the new number. The new number is a list,
so we need to take the sine of a list of numbers. Again MATLAB is
smart enough to know how to do this:
>> sin(pi*x) % finds the sine of each element
- Finally we need to take the square. We can think of this as
multiplying two lists of numbers. How do we want this to be
done? Now it gets interesting. In linear algebra there is a very
common way to multiply vectors (or lists) called the
dot-product
. Here is
an example:
(1,2,3) · (1,3,5) = 1 · 1 + 2 · 3 + 3 · 5 = 22Notice, you match up the corresponding terms, multiply these and then add. This is the default way that MATLAB multiplies matrices .
We want something different: We want to match up corresponding terms, multiply and get a list when all is said and done. To do this in MATLAB you tell the multiplication to work ``element by element''. The special command for this is a ``.'': a period or a ``dot''. Here's how it works with the simple example above:>> [1,2,3] * [1,3,5] % gives an error >> [1,2,3] * [1,3,5]' % returns 22. the ' is transpose % (this is the dot product) >> [1,2,3] .* [1,3,5] % what we want a list ans = 1 6 15which is the list [1,6,15]. To multiply we put a ``.'' in front. As well this is necessary for division ./ and exponentiation (.^). Thus our plotting commands could be:>> x = linspace(0,2*pi); >> y = (sin(pi*x)).^2; % using the .^ notation as the % sin(pi*x) is a list >> plot(x,y); % enough already, make the plot
-
multiply x by p. This is a number times a list. MATLAB does
this as you would expect
3.2 Numbers and lists in MATLAB
The language of MATLAB is taken from that of Linear Algebra. It is important to understand a few different types of data. First we are all familiar with numbers. You should know the difference between the integers, the rational numbers, the real numbers and you may know the complex numbers. In linear algebra of MATLAB we call these scalars .Why do we need to give these a separate name? We also want to talk about lists or arrays of numbers. In Linear Algebra we may call these lists vectors . There is a mathematical connection made between a vector, which is a way to represent a magnitude and a direction, and a point on the graph. This is why MATLAB uses coordinates to represent vectors. An example might be the coordinates of a point on the graph: (4,5), or in 3 dimensions (3,4,5). Or, a list of x-coordinates that we wish to find the y coordinates for. As well, we can use a list as a shortcut to represent polynomials: for example f(x)= 5x2 - 6x + 12 could be associated with the list (5,-6,12).
This is really confusing if you are not careful. Let's look at a table of some different ways a mathematician like yourself can think of the list of numbers (1,2):
| (1,2) | the point (1,2) in the Cartesian plane |
| (1,2) | the vector associated with the directed line segment (0,0),(1,2) |
| á 1,2ñ | the same vector, only in another notation |
| [1,2] | the MATLAB notation for a row vector |
| [1;2] | the MATLAB notation for a column vector |
| [1,2] | a coding for the polynomial 1x + 2 |
| [1,2] | a way to represent the equation 1x = 2 in linear algebra |
We can also speak of two-dimensional arrays of data, much like the way we reference elements of a spread sheet. We may need two indices to speak about something: such as the first column and 2nd row has a value of 10. In shorthand we might write something like a21=10 and understand this to be shorthand for what we have in mind. Such things are referred to as matrices . Another example might be if we have two lists, say 10 x-coordinates and 10 y-coordinates. Then we might want the 8th x coordinate or the 6th y-coordinate. These could easily be referred to by a81 or a62. a final example is to represent a system of equations.
Example: The system of equations
| 7x + 5y + 0.1 z | = 100 |
| x + y + z | = 100 |
|
Now for the fun stuff. We may want to multiply these things together. You should be familiar with addition, subtraction, multiplication and division of numbers or scalars, but you might be surprised to know there are ways of doing such combinations to vectors and matrices as well that are important in many areas of mathematics.
You may ask ``How do we tell MATLAB that we are multiplying a scalar times a vector, or how do we tell MATLAB that we are multiplying a vector times a vector''. MATLAB is as smart as it can be about guessing, but you will have to supply the answer in some cases.
In particular, if in doubt MATLAB will assume you are referring to a matrix. So to really understand how MATLAB works, you need to know what matrix operations are.
3.3 Numbers or scalars
First we need to understand operations between scalars. This is easy as it is simply the arithmetic we are all familiar with.3.3.1 Usual Arithmetic
The simplest MATLAB commands are arithmetic operations which are the familiar operations of your calculator. These are represented by the following symbols: addition (+), subtraction (-),
multiplication (*), division (/), and exponentiation
(^). Try the following commands and observe the MATLAB
responses. After typing each line below remember to hit the
enter key to put MATLAB to work.
>> 3+4 % ans = 7 >> 5*9 % ans = 45 >> 8/9 % ans = 0.8889 >> 5^3 % ans = 125 >> sin(pi) % ans = 0. pi is the constant 3.14...Even better than a calculator, just like in Calculus, we can can make assignment statements to simplify or organize our work. here are some examples:
Example: Assignment to variables
>> a = 7; % the variable a is now 7
>> b = 2; a = 5; % b is 2, and now a is 5
>> c = a - 2; % c is now 5-2 or 3
>> a = a + 1 % a common computer statement.
% a is now 5 + 1 or 6
>> a,b,c % easy as a,b,c -- prints them out.
>> e = exp(0) % e is now e^1=2.71.... (no built-in
% constant like pi)
>> log(e) % ans = 0
>> x = 2;h=.01 % define some variables
>> fx = x^2; fxh = (x+h)^2 % f(x) = x^2, fx=f(x), fxh=f(x+h)
>> slope = ( fxh - fx )/h % slope of secant line
>> r = 5; % define the radius
>> area = pi * r^2; % area of a circle
>> r = 2.5; % oops before we had the diameter
>> area = pi * r^2; % We don't need to retype
% use th up-arrow
>> clear(a) % clears out the a variable
>> clear % clears out all variables
A few comments:
- Since spaces are ignored its a good idea to make your lines easy to
read
>> difficult=exp(sin(x^2-5*x+6*(4-3))) >> easy = exp( sin( x^2 - 5*x + 6*(4 - 3))) % trust us!
- If a command is followed by a semicolon (;) then MATLAB carries
out the operation but the result will not appear on the screen.
- Once a value is assigned to a variable, MATLAB remembers it until that variable is reassigned or cleared.
3.3.2 Order of Operations
First a ``quick and dirty'' answer, then a more thorough one.When you have a sequence of operations, it is always possible to force them to be performed in a certain order by using parentheses. For example, (5-2)/6 = 3/6=2, or 5-(2/6) = 5 - (1/3) = 14/3. However, one often wants to omit parentheses to avoid typing. MATLAB uses the standard order of priority (precedence) for operations: addition and subtraction have the same priority, as do multiplication and division. Exponentiation has higher priority.
Example: First assign values to a, b, and c as described above. For example:
>> a=8; b=2; c=16;Then we verify
Command Numerical Answer in Math language >> a - b * c -24 a - (b * c ) >> (a - b) * c 96 (a-b)*c >> a / b / c .25 (a/b)/c >> a / (b / c) 64 a/(b/c) >> a ^ b * c 1024 (a^b)*c >> a ^ (b * c) 7.9228e+28 a^(b*c) >> a ^ b ^ c Inf a^(b^c)To see a more detailed explanation read on.
MATLAB uses the following symbols for arithmetic operations:
| Operation | Symbol | Precedence | Comment |
| Exponentiation | ^ | 3 | Highest precedence |
| Multiplication | * | 2 | |
| Division | / | 2 | |
| Addition | + | 1 | |
| Subtraction | - | 1 | Lowest precedence |
If an arithmetic expression contains nested parentheses, then the expressions contained within the innermost parentheses are evaluated first. In the absence of parentheses, the precedence rules decide the order of evaluation. The following rules apply:
1. All operations with a higher precedence are carried out before those of lower precedences. Thus exponentiation is carried out first, then comes multiplication and division, and finally, addition and subtraction.
2. If two operations have the same precedence then the operation on the left is carried out first. This is called the left-to-right scan rule.
The examples in the following table show how the precedence rules help interpret arithmetic expressions based on these rules. Try them out on the computer and make sure that you understand how each expression is interpreted.
| Expression | MATLAB value | Interpreted as |
2*3+4*5 |
26 | (2*3)+(4*5) |
2+3*4 |
14 | 2+(3*4) |
(2+3)*4 |
20 | parentheses decides the order |
2/5*4 |
1.6 | (2/5)*4 |
2/(5*4) |
0.1 | parentheses decides the order |
2\^{}3\^{}2 |
64 | (2^3)^2 |
2\^{}(3\^{}2) |
512 | parentheses decides the order |
5/2/4 |
0.625 | (5/2)/4 |
5/(2/4) |
10 | parentheses decides the order |
3.4 Lists or vectors
What is a list or vector ? In MATLAB and linear algebra they are a way to keep track of several values at once. Here is how we can generate them:Example: How to generate lists
w = [1,3,5,7]; % the list 1,3,5,7
x = [1;3;5;7]; % take a peek at x and w to see the
% difference. A column vector!
y = 1:2:7; % again the list 1,3,5,7
z = linspace(1,7,4); % one more time
To generate w and x we used the MATLAB command to
specify a list member by member. The commas create a row
vector
, the semi-colons create a column
vector
. Take
a peek at the values of w and x to see the difference.To generate y we use the colon-operator , a shorthand way to generate evenly spaced values. The format is a:h:b. Which generates evenly spaced numbers starting from a to b in steps of size h. Finally, z is generated using the linspace command which by default generates 100 evenly spaced values between the two points given, in this case 1 and 7. By using a third argument, we specified the number of points, in this case 4.
For more details go click below:
3.4.1 Generating lists of data
We will see how generate lists of data. To be specific, we will call a list of data a vector .- Entering specific numbers
Example: Suppose you have a list of jogging times as follows: 30.45, 29.54, 31.16, 42.33 in minutes and seconds. To store these in a list we could type the following:>> times = [30.45, 29.54, 31.16, 42.33] % notice the [] and the commas , times = 30.450 29.540 31.160 42.330 % a row of numbers
or>> runs = [30.45; 29.54; 31.16; 42.33] % notice the semicolon ; runs = % a column of numbers 30.450 29.540 31.160 42.330There is a distinction made in MATLAB between rows of numbers and columns of numbers (row vectors and column vectors). MATLAB can switch between them with the transpose operator ' for example>> runs' % notice the ' sign runs = 30.450 29.540 31.160 42.330 % a row of numbers
The transpose operator can be useful when displaying your data.
- Extracting data
Suppose I have times entered in above, and I want to know the 1st jogging time. I can get at this as follows:>> times(1) % returns 30.450 >> times(3) % returns 31.160 >> times([1,3]) % returns 30.450 and 31.160
The last line uses a slice of the vector. It finds the 1st and 3rd times. This can be useful.
Example: Suppose we want to plot the line connecting (1,2) to (5,7). To plot the line we may want to enter the data as a table:>> x=[1,5];y=[2,7]; % the x-values and y-values
The command>> plot(x,y)
would plot a straight line segment between the points (1,2) and (5,7). What is its slopem = ( y(2) - y(1) )/ ( x(2) - x(1) ) % m = (7 - 2)/(5 - 1) = 1.2500
- evenly spaced numbers
If you had to enter the number 1 through 5 into a list you could
type
x = [1,2,3,4,5]
which isn't too bad, but suppose you had to do 1 through 100. You'd want a shortcut. Fortunately there is one using the colon-operator :x = 1:5 % same as x = [1,2,3,4,5]
The colon-operator creates a row vector .
If one wanted the even numbers between 1 and 10, we can do this easily as well using the colon-operator>> x = 1:2:10 % steps by 2. gives 1,3,5,7,9
The inside 2 means go in steps of size 2 starting from 1 until we get to 10 or bigger.
Noting that these are 5 evenly spaced numbers between 1 and 9, we could also use the linspace command>> linspace(1,9,4) % 4 is optional, without it you get % 100 numbersWhat is the 10th odd number? We could find this without thinking by>> x = 1:2:100; x(10) % x = 19
First, we need to understand Addition, Subtraction, Multiplication and Division between a scalar and a vector (or list).
For concreteness, lets define two variables, one will be a scalar , the other a list or vector :
>> x = 5; y = [1,2,3];The output is suppressed due to the ; at the end of each command.
Now lets look at each case:
-
addition What is x + y? This is a scalar plus a
vector. In linear algebra this isn't defined, but MATLAB says what the
heck you must mean we add the value of the scalar to each value of
the vector. So:
>> x + y % adds x to each value in y. Same with y + x ans = 6 7 8
- subtraction. Just like addition:
>> x - y % y - x subtracts 5 from each 1,2,3 ans = 4 3 2
- multiplication. This is scalar multiplication from
linear algebra. Each element of the vector is multiplied by the
scalar:
>> x*y % same as y * x ans = 5 10 15
Notice we use the ``*'' symbol for multiplication, just like usual. - division. Now we have to be careful. First dividing a
vector
by a
scalar
is what we expect -- each element
in the list is divided by the scalar
>> y/x; % gives ans = 0.20000 0.40000 0.60000
What about a scalar divided by a list? Let's try it:>> x/y % scalar divided by a list Warning: Warning: Will Rogers % MATLAB chews you out somehow
What went wrong? In Linear Algebra you can't divide by a vector . We'll see more on this later, but you may want to use the dot-operator . (>> x ./ y).
First for concreteness lets define some variables
>> w = [1,3,5,7]; % the row vector 1,3,5,7
>> x = [1;3;5;7]; % the column vector
>> y = linspace(1,7); % a list of numbers between 1 and 7 --
% a 100 numbers evenly spaced
-
addition and subtraction. What do we want. We have that
2*w is a vector whose entries are twice that of w,
so w+w should be the same: vector addition adds the
corresponding entries, keeping a vector for the answer.
>> w + w ans = 2 6 10 14
However trying to add w + x or w + y will give errors. In the first case the vectors have the same number of elements but are different shapes (a row vector and column vector). In the second case the vectors have a mismatched number of elements (w has 4 and y has 100)
moral number 1: to add or subtract vectors they must have the same shape and number of elements
moral number 2: If you try to add or subtract a vector and MATLAB chews you out, refer to moral number 1. - multiplication. There are two different multiplications
possible. One is the
dot product
the other is an element by
element product. The dot product can be viewed as a form of
matrix multiplication
-
dot product Its called the dot product because many
textbooks use a dot to represent it. For MATLAB it is a specific
case of matrix multiplication. To do the dot product we need two
vectors with the same number of elements, but the first one needs
to be a column vector and the second a row vector. (This is no
concern, because the
transpose-operator
'
switches back and forth.) We have w is a row vector and
x is a column vector. To do the dot product we write it
as usual multiplication
>> w * x % or used dot command ans = 84
Mathematically this took the matching elements in w and x and multiplied them, then added. Check that 84 = 1· 1+ 3 · 3 + 5 · 5 + 7 · 7.
- Element by element product.
If we want to multiply two lists ``element by element'' then we have to override MATLABs desire to do matrix multiplication. The dot-operator does this.
Example: squaring lists of numbers
Suppose we have a list of data representing measurements of radiuses of pipes, and we wanted to find the cross-sectional area of each one. That is we want to square and multiply by p. we could achieve this by>> rad = [12.2, 12.5, 12.0, 11.8]; % our data set >> rad2 = rad .* rad % the square. Could have been: % rad.^2. Notice the dot! >> area = pi * rad2 % or in one line: area = pi*(rad.^2)To use the dot-operator we need to have lists that are the same shape and size.
-
dot product Its called the dot product because many
textbooks use a dot to represent it. For MATLAB it is a specific
case of matrix multiplication. To do the dot product we need two
vectors with the same number of elements, but the first one needs
to be a column vector and the second a row vector. (This is no
concern, because the
transpose-operator
'
switches back and forth.) We have w is a row vector and
x is a column vector. To do the dot product we write it
as usual multiplication
Example:
>> a = 1 : 1 : 5 % creates array a = [1,2,3,4,5] >> b = 1 : 2 : 9 % creates array b = [1,3,5,7,9] >> a + b % vector addition -- no ``.'' needed ans = 2 5 8 11 14 >> 3*a - b % scalar multiplication. no ``.'' needed ans = 2 3 4 5 6 >> a * b % need a dot, or MATLAB will complain ERROR! That it not logical Spock! >> a.*b % notice the dot ans = 1 6 15 28 45Element by element multiplication, division and powers require a special dot operation: ``*'', "/", or ".^"
Example:
>> a./b % division needs the ``.'' ans = 1.0000, 0.6667, 0.6000, 0.5714, 0.5556 >> a.^2 % So does taking powers! ans = 1, 4, 9, 16, 25The dot preceding the asterisk or the slash or the symbol
`^' tells MATLAB to perform element by element array
multiplication, division, or exponentiation respectively.
Here are some additional examples where array mathematics have been used:Example:
Plot y=sin x + cos 3x over the domain [-p,2p] using steps of p /100:
>> x = -pi : pi/100 : 2*pi; y = sin(x)+cos(3*x); plot(x,y),gridNotice there is no need for a dot as we didn't use multiplication, division, or exponentiation of a list.
Example: Plot y = e-x/2cos 6x over the domain [0,p]:
>> x = linspace(0,pi); % or, x=0:pi/100:pi;
% or even (0:100)*(pi/100)
>> y1 = exp(-x/2); % built in function okay without dot
>> y2 = cos(6*x); % or, y = (e(-x/2)).*(cos(6*x))
>> y = y1.*y2; % need that dot for multiplication
>> plot(x,y),grid
Again note that the dot: ``.'' before the * means that
multiplication of the two arrays y1 and y2 is to be carried
out element-by-element. That is, each element of y is obtained by
multiplying the corresponding elements of y1 and y2.
Example: Plot y = x3 over the domain [-1,1]:
>> x = -1 : .05 : 1; % or use linspace >> y = x.^3; % we need that dot! its a power >> plot(x,y)
Note again that the dot before the exponentiation means that each element of the x array must be raised to the third power.
Example: Here is a special example about the syntax of MATLAB. Try this without the parentheses around the 1 before the ./ to see an error message.
Plot y = 1/(x2-1) over the domain [-2,2]:
>> x = -2 : 0.1 : 2; >> y = (1)./(x.^2-1); >> plot(x,y), grid % notice the discontinuities
You must put the parentheses around the 1 to prevent MATLAB from reading this as
>> y = 1.0/(x.^2 -1) % dividing by a list needs a dot!! Try again Homer!You could avoid having to think this out, if you remember that 1/x = x-1 and use
>> (x.^2 -1).^(-1) % double dots!
4 Symbolic Math
This section needs to be written.5 Functions
There are several ways you can use functions in MATLAB. There are built-in functions such as the sine and cosine functions, there are special means to deal with polynomials, there is the ability to work with symbolic functions and you can define your own functions using function m-files.5.1 Built-in functions
Listed below are some of the basic functions built into MATLAB.First the standard trigonometric functions , exponential functions and logarithmic functions.
Here are some functions that make the display of numbers nicer:
- format . Typical ones can be either short, long, or rat. For example the command >> format rat will cause the display to use fractions when appropriate
-
colon-operator
the construct
a:h:bwe'll call the semicolon operator. It generates a vector of numbers between a and b of step size h. - cross
The cross command find the
cross product
between 2 three-dimensional vectors.
- dot The dot command find the dot product between two vectors.
- dot-operator
The ``dot'' or period before an operator
such as * for multiplication, or ``/'' for
division or ``^'' for exponentiation. Tells MATLAB to
operate ``element by element'' or ``point by point''. For an example
look at a
dot operator example
- help The help command accesses MATLAB's built-in help facility. To try it out try the command: help plot.
- prod
The prod command takes the product of a
list of numbers, when given a matrix it takes the product of each
column returning a column vector. Here is how one could implement
the factorial command, n!:
>> n = 10; prod(1:n) % returns 10! = 3628800 = 10*9*8*...*1
- roots
The roots command find zeroes of a
polynomial. Click here to see
an example.
- sum
The sum command adds the entries in a
list or the columns in a matrix. For example, let's see that the sum
1 + 22 + 32 + ··· + n2 is a perfect square when n = 24.
>> n=1:24; % thenumber 1 through 24 >> a = sum(n.^2); % need a dot as n is a list >> sqrt(a) ans = 70 % a perfect square
Except for n=1 this is the only n for which this is true. Here is an example to simulate the number of heads in 100 coin tosses 250 times.>> r = rand(100,250); % 100 random numbers in [0,1] 250 times >> r = floor(r+.5); % takes integer part of r + .5 % this is a number 0 or 1 with equal % chance >> a = sum(r); % adds down the columns, giving 250 % numbers >> hist(a); % plot a histogram -- bell shaped - transpose-operator the symbol ' or single-quote indicates transpose. It switches a row vector into a column vector or vice versa.
- cylinder
Despite its name, this command plots a surface
of revolution of a curve around the z-axis. The curve is entered
in a vector of radius values. (That is you plot the surface given by
x2 + y2 = f(z)2.) To plot a sphere you could enter the
commands
>> z = -1:.1:1; >> r = sqrt(1 - z.^2); >> cylinder(r).
- grid puts a grid up during a plot command.
- linspace
The command linspace(a,b,n) generates
n points equally spaced over the closed interval [a,b]. Note that if
you wish to divide an interval into 10 equal subintervals, you need
11 points including the end points of the interval. If you omit
n then the command linspace(a,b) generates 100
equally spaced points over [a,b]. Similar to
colon-operator
.
- meshgrid
Like the
linspace
command, this
creates a matrix of x and y values to be used in plotting
three-dimensional graphs. It is used in the following manner:
>> [x,y] = meshgrid(-1:.1:1,-pi,:.1,pi);
- plot The plot command is used to plot lists of data. In its simplest use if x and y are the same size list, then plot(x,y) plots the x list verse the y list. More advanced features are possible. See the help page or click here.
- plot3 The three-dimensional plotting function. The command plots3(x,y,z) plots the points (xi,yi,zi) with a straight line connecting the point (xi,yi,zi) to (xi+1,yi+1,zi+1).
- sphere
Will plot a sphere. See
help spherefor more info. - surf
Creates a graph of a surface. It is called by
>> surf(x,y,z), where x, y and z are matrices. To use it you would typically create the values of x and y with the meshgrid command, and the value of z as a function of x and y. - view
This command changes the view or perspective of a
three dimensional graph. You can call it with two angles or a
vector. The vector is a three-dimensional vector that points in the
opposite direction than where you are looking from. For example,
view([1,1,1])will give a view of the origin as if you are looking from the point (1,1,1). - zoom The zoom command is usually followed by either an on or off. When on it allows you to explore the current plot with your mouse. ``Dragging'' out a window will force MATLAB to ``zoom in'' on that area. To undo this double click the mouse. As well, clicking in an area will force a similar effect.
5.2 Polynomials
There are a number of MATLAB commands that allow one to work easily with polynomials. For example: conv , deconv , poly , polyder , polyfit , polyval , roots . See the help commands if you can't find a definition.To use any of these built-in functions you need to be familiar with the shorthand convention MATLAB uses to store polynomials. Since a polynomial is determined by its coefficients (why?), it is only necessary to keep track of these numbers not the powers of x. For example, 15x3 - 6x + 12 is associated with the list (15,0,-6,12). Now a list in MATLAB can be a row vector or a column vector. MATLAB takes the convention that polynomials will be row vectors so the polynomial above would be
p = [15,0,-6,12] % notice commas not semicolons -- row vectorIf we wanted to find the roots of the polynomial 15x3 - 6x + 12, or the solutions to the equation 15x3 - 6x + 12=0 we could use the MATLAB command roots as follows
>> roots(p) % notice answer is a column vector ans = -1.07097 + 0.00000i % this is the real number -1.07097 0.53549 + 0.67841i % these two are complex conjugates 0.53549 - 0.67841iA general fact about polynomials tells us that a 3rd degree polynomial will have 3 roots. So we start with a row vector with 4 entries, and we get back a column vector with 3 entries.
5.3 Function m-files
If you want to explore many functions, it is tedious to keep retyping and/or using the Up Arrow key to repeat commands. Here we learn to simplify our work with script files and m-files .A script file will be a file that stores a sequence of keystrokes that makes it easier to reuse, or easier to edit if it is complicated.
An m-file (or function m-file) in MATLAB is the way subroutines are implemented. Knowledge of how to create m-files can make MATLAB a very powerful tool for studying mathematics.
-
SAVING COMMAND SEQUENCES IN M-FILES OR SCRIPT FILES
if you are working on the CSI network, and you do not already have a diskette in drive A you need to inform MATLAB where to find your personal script files. Try the command>. path(path,'a:\'); % or restart MATLAB with diskette in a:
To create a new script file in Windows 3.1:- Open the file menu (by clicking on FILE on the menu bar with the left mouse button);
- click on NEW in the menu; a sub menu will appear;
- click on the M-FILE option.
This will open a new untitled file in the Notepad editor (it is possible to set up MATLAB to use other editors). You should resize and arrange your windows so that it is easy to go back and forth between the MATLAB Command window and the Notepad window.
- You are know ready to go!
Script file exampleeg:script-file
Type in the following lines in the Notepad window. (Nothing will happen in the MATLAB window.) After typing a couple lines, choose Save As from the Notepad File menu. Save the file under the name ``limit.m'': you must use the extension ``.m'' or MATLAB will not recognize it. Choose Save from the File menu when you're done, but leave the Notepad window open. You will have written a program in the MATLAB language.
This program uses a shortcut: instead of writing x=[.1 .01 .001 ...], we write x=(.1).*(n) where n=1,2,3,...
%%%% this file should be saved as limit.m %%%% a % (percent sign) makes a comment to the end of the line clear % gets rid of old definitions format long % gives more digits in the answer n= 1:1:6; % the numbers 1 though 6 x=-(.1).^n; % the numbers 10^(-1) through 10^(-6) y=sin(x)./x; [x;y]' % limit from left in a table form x=(.1).^n; % or use x = -x with x above y=sin(x)./x; [x;y]' % limit from right in a table form
(Recall: MATLAB ignores text following a%.)
After saving the file, return to the MATLAB Command window (by clicking somewhere inside the window), and type>> limit % evaluates the file limit.m
Note that you don't type the ``.m''. MATLAB should begin to execute the commands just as if you had typed them in the Command window.
If you made an error while typing the file limit.m, MATLAB will halt on the line with the error and print out an error message. Simply return to the Notepad window, fix the error, Save the file, and try typinglimitagain in the Command window. If you already closed the Notepad window, Click on Open in the File menu (in the Command window), find limit.m in the file list and reopen the file.
Note: MATLAB does not find syntax errors before running the program since it uses an interpreter rather than a compiler (like C or Pascal).
moral: MATLAB beeps when it is trying to get your attention. This means it can't figure out what you mean. Pay attention and find out why it beeped, its just trying to help you.
- Function m-files
In order to create functions in MATLAB we need to have an understanding of how MATLAB handles the following computer related concepts
Format of the m-file: what is the syntax.- Input and Output of data: how to pass arguments
- looping: for loops
- Conditional expressions: how to direct the flow
- Calling the function from MATLAB.
Let's look first at an example to illustrate these points. The function n! in mathematics is shorthand for 1 · 2 ··· n. In MATLAB there is no built-in factorial function. Lets define one as fact. our function fact should have as its input a non-negative integer, and its output should be the factorial.function y = fact(n) % the function word is a non-comment. y % is the name of the output variable % and n is the name the m-file gives % to the input variable. if n < 0 % this line prints out an error message fprintf("factorial needs a non-negative integer\n"); % returns if there is an error return end y = 1; % initialize the value of y for i = 1:n % a loop y = y*i; end % end the loopLet's analyze the important lines.-
function y = fact(n)
This line follows the syntax of a function m-file. The first word if the keyword function. Then the return value or output, in this case the value of y. What does the return value equal, the function name without the .m extension, in this case fact, and then the input, in this case n. Hence when n is referred to in the file, it refers to the input value. -
if n < 0
This is the syntax for a conditional test. The simplest usage isif (CONDITION) THEN-BODY end
as in the factorial example. In general, it can beif (CONDITION) THEN-BODY elseif (CONDITION) ELSEIF-BODY else ELSE-BODY end
An example in general can be given with the heavyside function:function y = h(x) % save this a h.m if x < 0 y = -1; % so h(-5) = -1 elseif x = 0 y = 0; % h(0) = 0 elsif x > 0 % and h(5) = 1 y = 1; end
-
fprintf(stderr,"factorial needs a non-negative integer\n");
This is one way to pass a message back to MATLAB. The command fprintf is the print function, the word stderr tells MATLAB where to print the upcoming message (in this case where error messages go), and the line in quotes is the message. The\nis the end of line character.
-
for i = 1:n
This is main looping construct. This increases the value of i from 1 to n where n is the number given to fact when the function is called. The general syntax for a for loop isfor x = array COMMANDS end
Whew, that was a lot of work considering the following commands will find the factorial:
>> prod(1:n); % product of 1,2...n >> gamma(n+1); % gamma function is related to factorial
The array can be quite general. Here are some examples which can be run from the command line, or put into an m-file>> tot = 0; % our total >> for i = 1:2:100 % just the odd numbers > tot = tot + i; % you may have a different prompt >> end; tot % prints sum of odd numbers between 1 % and 99>> x = randn(1,100); % a list of 100 normally distributed % random numbers >> temp = 1:100; % the number 1 through 100 >> for i = temp(x < -2 | x > 2) % these are outliers in the data > x(i) = 0 % make outliers 0 >> endThe last example uses some a complicated way to get the array or list of numbers to index over. It takes only those indices for the list x which have x-values less than -2 or bigger than 2.
Another looping construct is the while command. This has the formwhile (CONDITION) BODY end
An simple example could be to construct the first n Fibonacci numbers. These numbers are 1,1,2,3,5,8,13,21,34,55 if n is 10.function fib = fib(n) % save as fib.m. return name same as % function name. That's okay! fib = ones (1, n); % fib = [1,1,1,1,1,1,1,1,1,1] if n=10 i = 3; while (i <= n) fib (i) = fib (i-1) + fib (i-2); % 1+1=2, 1+2=3, 2+3=5, 3+5=8 ... i=i+1; % increment i endThe while loops keeps looping until the condition that i be less than or equal to n is no longer true. The command ones is a simple way of making a sequence of all ones. Of course we should check that n is an integer bigger than 3. Don't forget to increment your expression or you'll find an infinite loop. (you can use the control-c key sequence to disable this.>> i = 1;while i < 2 > fprintf(``Help me! I'm stuck in an endless loop\n'') >> end
Some more examples of m-files:-
Evaluating functions from mathematics.
Suppose you wanted to evaluate the function f(x) several times in the course of a mathematical experiment. One way to type less is with an m-filefunction y = f(x) % save as f.m y = 1 - x.^2/2 + x.^4/4; % 5 terms in Taylor series for cosine % x. Notice the dotsThis was written so that both x and y could be lists of numbers. To use this we might do this in a MATLAB session>> x = linspace(0,pi); >> y = f(x);z=cos(x); % pass f(x) a list of numbers. No % problem. >> plot(x,y,x,z) % compare approximation to cosine x >> h=.01, difquo = (f(x+h) - f(x))/h % compute difference quotient >> plot(x,difquo,x,sin(x)) % compare difference quotient. - Writing your own
ezplot
.
Suppose you want to make plotting of a function simple, but you don't want to use ezplot as it works only for symbolic functions. Here is a simple m-file you could use. Can you think of any extensions you might make?function y = myezplot(f,a,b) %% myezplot: called with a function defined in an m-file, a and b %%graphs the function f defined in f.m over the range of %% values specified by the range [a,b]. If a and b are omitted it %% takes the interval [-5,5] as a default. if nargin = 1 a=-5;b=5 end for x = linspace(a,b) % loop over x in [a,b] y(i) = feval(f,i) % call the function in f.m. Needs to use % feval end plot(x,y);To call this function you would first define your function in a m-file, say yourfunc.m, then you would use the command>> myezplot(yourfunc,0,3) % plots yourfunc between 0 and 3
This example uses the variable nargin which is a count of the number of arguments in the input. As well it shows how you can pass a function name to a function. You need to use the command feval to evaluate the function.
6 Plotting functions
One of the most exciting uses of MATLAB is its ability to easily create the graph of a function. Suppose that we wish to plot the graph of the parabola y=x2 over the interval -2 £ x £ 2. How might we do this?If you wanted to plot this on a piece of paper, you might generate a table of numbers such as
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Then you would plot each point (x,y) and connect the values with a curve which seemed appropriate -- in this case a parabola. Let's call this way of plotting ``x vs. y''.
Another way you might want to plot is to simply tell the computer to plot the function ``x2''. The command to plot a symbolic function will be ezplot .
MATLAB knows of other types of plots as well:
- Parametric plots: these allow you to plot x versus y only,
these are
parameterized by a third variable say t for time. Here's an example of
plotting the circle:
x(t) = cos(t), y(t)=sin(t); -2 £ t £ 2.
>> t =linspace(0,2*pi); >> x = cos(t);y=sin(t); >> plot(x,y); % notice we define x and y interms of % t, but we plot x vs y - Polar plots: to plot in polar coordinates
- Three-dimensional plots: plotting x, y and z.
- makemenus : Adds nice menus to plotting window which allow you to add text to graphs easily, to rotate axes, and other things. You can read about it in this file makemenu.README. The files are available on the MATHWORKS website, or on the math department site. At the math department site the windows files are in makemenu.exe and the UNIX files are here makemenu.tar.
6.1 Plotting x versus y
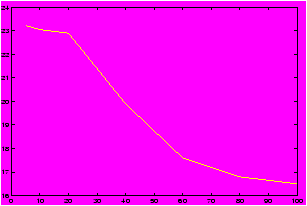
We see here how to plot functions, by plotting a table of values for x and y=f(x).Example: Cost of a used car
Suppose you were interested in buying a used car. You may want to know the relationship between number of miles the car has and the value of the car. Such numbers are available on the internet, for example these numbers were found at http://www.kbb.com. The price of a used 1996 Jeep Cherokee is figured according to the number of miles given. Here is some sample data:
| Mileage | Estimated Price |
| 5,000 | 23,225 |
| 10,000 | 23,050 |
| 20,000 | 22,900 |
| 40,000 | 19,900 |
| 60,000 | 17,600 |
| 80,000 | 16,800 |
| 100,000 | 16,500 |
>> mileage = [5,10,20,40,60,80,100]; % skip the thousands >> cost = [23.225, 23.050, 22.9, 19.9, 17.6, 16.8, 16.5]; % in thousands >> plot(mileage,cost)
From the graph we can see an interesting relationship not obvious from the table. For low, low mileage cars the graph is kind of flat prsumably as people believe the car is practically new, but as the mileage increases the cost decrease rapidly after a certain point. This may be explained by the realization that people shouldn't have to pay for the mileage already on the car, and the loss of warranty. The graph is more or less linear here. This eventually tails off as the mileage gets real high and the graph flattens out.
It is precisely the ability of plots or graphs to convey information quickly and clearly that makes them so invaluable. In this section you can learn how to create them.
6.1.1 Plotting lines
We all know that two points determine a line. What does this mean?We'll use MATLAB to plot the graph of a line using just two points.
First you may want to recall some basic formulas to describe lines:
Concept: Equations for lines
- The slope of a line:
Let (x1,y2), and
(x2,y2) be two points on a line. Then the slope of the line is
given by the rise over the run.
m = (y2-y1)/(x2-x1).
- Point-slope equation:
Let (x1,y1) be a
point on the line and m be its slope. Then the equation of the
line is
y = m (x - x1) + y1(Essentially you solve for y)
- Slope-intercept form:
Let m be the
slope and b be the y-intercept of a line (so (0,b) is a point
on the line) then
y = mx+b
- two points:
Let (x2,y2), and
(x1,y1) be two points on a line. Then
y = y2-y1 x2-x1 (x - x1) + y1
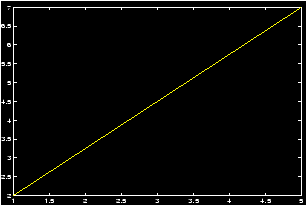
Example: For definiteness, we want to plot the line connecting (1,2) to (5,7). First lets define the points. How should we do this? Lets pair off the x values and the y values:
>> x=[1,5];y=[2,7];Now we can use MATLAB to reference the individual components if we need to. Notice how this is done:
>> x(1) ans = 1 >> y(2) ans = 7So we could compute the slope by
m = ( y(2) - y(1) )/ ( x(2) - x(1) )Or we could plot the line by
>> plot(x,y)
Notice this draws a line between our two points. What if we wanted to plot the line over a specified interval, say [0,5]. We have a slope, and a range of x values, and a point (1,2). Using the point-slope form we know we should use the formula y = m (x - x1) + y1. We know m and x1 and y1, what do we do with x and y?
When plotting, we need to make a table of values for x and a corresponding table of values for y. In MATLAB this is done by letting x be a list or vector or numbers and then creating y based on x. To do this we can use the linspace command:
>> x = linspace(0,5); % 100 evenly-space numbers between 0
% and 5
>> y = m * (x - x(1)) + y(1); % point-slope form
>> plot(x,y);
Example: plot of farenheit
Let's plot the relationship between farenheit and celsius. Recall the formula is F = 9/5 C + 32. The interesting range of values might be for celsius between 0 and 100.
>> celsius = linspace(0,100); % the domain >> farenheit = 9/5 * celsius + 32 % our formula >> plot(celsius,farenheit) % the plot >> hold on; >> plot(farenheit,celsius) % the inverse bunction
6.1.2 Plotting functions
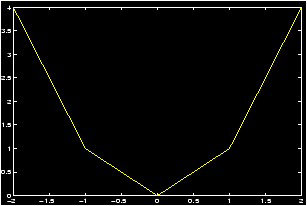
Suppose that we wish to plot the graph of the parabola y=x2 over the interval -2 £ x £ 2. In the absence of MATLAB, we could choose a set of x values, say, x=-2,-1,0,1,2, then square each x value to determine the corresponding y values, y=4,1,0,1,4. We then mark each corresponding (x,y) pair as a point on a Cartesian coordinate system. These pairs are {(-2,4),(-1,1),(0,0),(1,1),(2,4)}. Finally, we try to connect these points smoothly to obtain a sketch of the parabola. To create a graph of y=x2 using only the same 5 points as described above, we can issue the following MATLAB commands.>> x=-2:1:2; % creates the array x=[-2 -1 0 1 2] >> y=x.^2; % creates the array y=[ 4 1 0 1 4]; note the ``dot" after x >> plot(x,y)
A brief explanation is in order. The first line defines x to be the list (or row vector ) of values starting with -2, continuing in steps of 1, and ending at 2. (This uses the colon operator .) The second line defines y as the array of values which are the squares of the x values. That is, the y list is obtained by squaring the x list element-by-element. See a description here of the dot operator ).
What you see should be a crude graph of the function y=x2 consisting of a sequence of broken lines connecting the (x,y) points calculated. To create the graph, MATLAB simply starts with the first point, connects it with a straight line to the second point, and connects the second point with a straight line to the third point, and so on. Thus every graph in MATLAB consists of a sequence of straight lines.
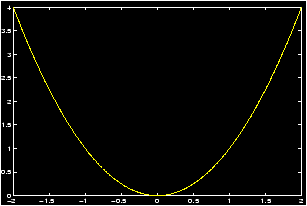
If you wish to obtain a smoother graph, all you have to do is use more points. But this requires no more labor on your part than using just 5 points. The following commands should create a much smoother graph as they utilize 201 points to construct the graph. Although it may no longer be evident, the graph still consists of a sequence of straight lines!
>> x=-2:0.01:2; % creates the array x=[-2 -1.9900 -1.9800 ... 1.9900 2] >> y=x.^2; % creates the array y=[ 4 3.9601 3.9201 ... 3.9601 4] >> plot(x,y)
Graphing functions -- more details
Here are a number of different examples of how we can use MATLAB to plot functions.
- Continuous Functions
A function f(x) is a set of ordered pairs (x,y) such that y=f(x). To create a graph of this function we first form two lists x=[x1,x2,...,xn], and y=[y1,y2,...,yn] where yi=f(xi), i=1,2,···,n and then issue the MATLAB command plot .
Example: Plot of y=ex
As an example, let us create a graph of the function y=ex describing each step in detail.
First decide the domain of the function and the desired frequency of plot points. Suppose that we let x vary from -1 to +1 in steps of 0.2. This is accomplished by the command:>> x = -1 : 0.2 : 1; % or use linspace(-1,1,11)
This creates an array with 11 elements starting at x = -1, increasing steps of .2 and ending at x = 1. If you do not type the `;' at the end of the command line you can see the array created asx = [-1, -.8, -.6, -.4, -.2, 0, .2, .4, .6, .8, 1]
Recall (Generating lists of data) for the explanation of the colon operator . (thatx=a:h:bgenerates an array of values starting at x=a, increasing in steps of `h' without exceeding x=b. Thus, this command will divide the interval [a, b] into n equal parts (n = (b - a)/h), thus sampling the domain at (n + 1) points including the two end points.
- For each value of x, calculate the corresponding value of
y. This is accomplished by the command:
>> y = exp(x);
Note that the built-in function exp(x) is defined such that if the argument x is an array, then it generates an array y of function values corresponding to each of the x values. Thus, y is now an array of 11 elements. If the semicolon at the end of the line is omitted you will see this array as:y = [.3679, .4493, .5488, .8187, 1.0000, 1.2214, 1.4918, 1.8221, 2.2255, 2.7183] - To obtain a continuous plot of ex over the domain
[-1,1], issue the command
>> plot(x,y)
The desired continuous graph will be created on the screen. Here, continuous plot means that MATLAB marks each ordered pair (xi,yi), i=0,1,2,...,n on the graph and then connects, by a straight line, the point (x0,y0) to (x1,y1), the point (x1,y1) to (x2,y2), and so on until the point (xn,yn) is reached. This graph created with 11 sample points is obviously not so smooth. Thus to obtain a smooth looking curve one needs to take sufficiently many x points depending on how rapidly the function varies over its domain. The following three commands may be used to obtain a smoother graph;>> x = -1 : 0.01 : 1 ; y = exp(x) ; plot(x,y),grid
We have added a grid command at the end to produce a set of grid lines on the graph. Note that we have used a smaller step size of 0.01 giving us 201 (2/.01 = 200) sampled points and therefore a much smoother graph.
-
Discrete plots
At times, instead of a continuous plot we may wish to obtain a discrete plot or point plot whereby the points are marked on the graph but they are not connected to each other by straight lines. In that case we need to specify the symbol we wish to use to mark each point. Supposing that the symbol is`*', the plot command becomes>> plot(x,y,`*')
Try this and see what happens.
MATLAB permits only a limited number of symbols to be used in discrete plot s. These are the symbols *, `.', `+',`x',`o'.
Example: Discrete Plots
To see the discrete points distinctly, you should use a reduced number of sample points, by taking a larger step size:>> x=-1:0.2:1; y=exp(x); plot(x,y,`*'), grid
which will produce a discrete graph with exactly 11 points.
A convenient way to control the number of points on a graph without calculating the corresponding step size over the domain of definition is to use the built-in function linspace . Using this function, the above graph can be obtained by entering>> x=linspace(-1,1,11); y=exp(x); plot(x,y,`*'), grid
More generally, the commandx=linspace(a,b,n);generates n points equally spaced over the closed interval [a,b]. Note that if you wish to divide an interval into 10 equal subintervals, you need 11 points including the end points of the interval. If you omitnthen the commandlinspace(a,b)generates 100 equally spaced points over [a,b].
- GRAPHING MORE THAN ONE FUNCTION ON THE SAME GRAPH
You can plot more than one function at a time by using the plot command in a extended way.
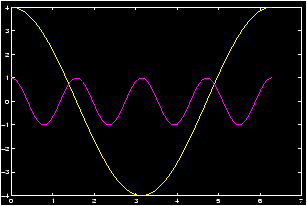
Example: Amplitude vs. Period
Let's investigate the relationship between the amplitude and the period for the cosine function. Recall
Concept: the generic form of a cosine function
y = a + d cos(b x + c).- The value of a determines the shift up or down the y-axis
- The value of |d| is the amplitude.
- The value of b determines the period by the formula T = 2p/b.
- The value of c determines the phase shift. (it is not c, but rather c/b.
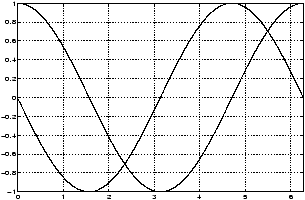
>> x=0:pi/100:2*pi; y1=4*cos(x); y2=cos(4*x); plot(x,y1,x,y2), grid
By giving MATLAB data in this form it knows to graph both functions. Note that MATLAB decides a frame which fits in all function values, and then creates a plot of each function. If you have a color monitor, different colors will be used for each function.
Another way to achieve this is with the hold function:>> x=0:pi/100:2*pi; y1=4*cos(x); y2=cos(4*x); >> hold on; % prevents second graph >> plot(x,y1), grid % from over-writing the >> plot(x,y2) % first
The hold command has two uses hold on or hold off. This toggles whether or not MATLAB will try to draw the next graph without erasing the previous one.
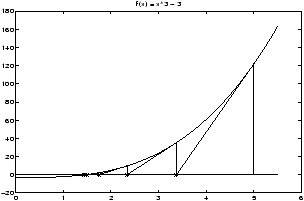
Example: Secant line example
Concept: Definition of the secant line
The secant line is the beginning of the study of derivatives in calculus. It involves lines, and their slopes. The fundamental thing to know is the following definition:
The limit of the slope of the secant line (if it exists) is the derivative of the function.
Let y=f(x) be a function and let x1,x2 be two points in its domain and consider the secant line connecting the two points P1=(x1,f(x1)) and P2=(x2,f(x2)) on the graph of this function. The slope of this secant line is given bym=(f(x2)-f(x1))/(x2-x1).
This represents the average slope of the function f(x) on the interval [x1, x2].
Another way we see this written is to let h = x2 - x1 be the difference between the two points x2 and x1. Then the formula for the slope becomes
m=(f(x1+h)-f(x1))/h,
and the derivative of f(x) at the point x1 is given byf'(x1) = lim h® 0 (f(x1+h)-f(x1))/h.
To see the secant line and the function on the same graph, we need to plot both functions simultaneously. This is done via the hold command: Let f(x) = sin(x), and let x1 = p/4, and x2 = x1 + h where h = p/8. We'll plot the secant line and the function between 0 and p/2.>> x1=pi/4;h=pi/8;x=linspace(0,pi/2); % assign the constants >> m = (sin(x1+h) - sin(x1))/h; % find the slope >> ysin = sin(x); % the y values for f(x) >> yline = m*(x-x1) + sin(x1) % point-slope form of a line >> hold on; % turn on hold >> plot(x,ysin) % plots the function >> plot(x,xline) % plots the line
You should see both plots on the graph.
- GRAPHING FUNCTIONS OVER DOMAINS WITH DELETED POINT(S)
When we do not have a continuous function then we have to do more work to plot it with MATLAB.
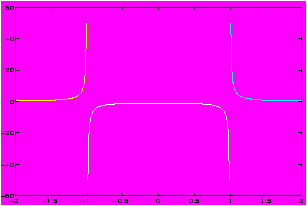
Example: Deleted points in the domain
Plot f(x) =1/(x2-1) over [0,2]: Notice the function f(x) is a discontinuous function at x=1. First try typing:>> x = 0 : 0.05 : 2; y = (1)./(x.^2-1);^ plot(x,y), grid
What does the graph look like?
The function is undefined at x = 1. In processing you can avoid that point by dividing the domain into two parts. Notice we avoid the point x=1.>> x1 = 0 : 0.05 : 0.95; y1 = (1)./(x1.^2-1); >> x2 = 1.05 : 0.05 : 2; y2 = (1)./(x2.^2-1); >> plot(x1,y1,x2,y2),grid
Mathematically, we plotted the following function:f(x) = (x2 -1)-1 if x ¹ 0, f(0)=0.f(x) = ì
í
î1/(x2-1) 0 £ x < 1 1/(x2-1) 1 < x £ 2
- PLOTTING FUNCTIONS DEFINED BY MORE THAN ONE EQUATION
Many functions in Mathematics need to be defined in a piece-by-piece fashion. For example the absolute value function, or the greatest-integer function. To plot these we have to use MATLAB in a piece by piece fashion as well
Example: The sign function
Plot the following function, sometimes called the, sign function, over the interval [-3,3] defined as followsf(x) = ì
í
î|x| / x if x ¹ 0, 0 if x = 0
f(x) = |x|/x if x ¹ 0, f(0) = 0.
Define>> x1=linspace(-3,0); y1=abs(x1)./x1; % -3<x<0 >> x2=linspace(0,3); y2=abs(x2)./x2; % 0<x<-3 >> plot(x1,y1,0,0,'*',x2,y2), grid
Note that in the plot command, the single point at the origin is being marked with a `*' to make it visible. This one is not well suited for the hold command.
6.2 plotting with ezplot
6.3 Parametric plots
6.4 Polar plots
6.5 Three-dimensional plots
MATLAB has some abilities to work with 3-dimensional plots. In this section you can learn how to plot- a vector as a line segment.
- a plane in 3 dimensions.
- a cylinder , which mathematically speaking is more complex than your last can of Coke.
- surfaces of revolution .
- a vector-valued function as a parameterized curve.
- Functions of the form z = f(x,y).
You may find the makemenus m-files to be of use with manipulating the graphing window. Among other things, these allow you to use the mouse to rotate the viewing angle.
6.5.1 Three-dimensional plotting functions
To plot with three dimensions we use the following built-in MATLAB functions: meshgrid , plot3 , surf , view , sphere , cylinder .As well, we will define several short m-files that facilitate the plotting process. These use the MATLAB commands above to plot.
6.5.2 Plotting vectors
Plotting vectors is as easy as connecting two points with a line. Recall in two dimensions, to connect two points we use the plot command. An example is given here>> plot([1,5],[2,7]);This plots the line between the points (1,2) and (5,7). In other words, the command plot(x,y) plots the list of numbers in x versus those in y connecting the points (xi,yi) to the points (xi+1,yi+1). The plot3 command does exactly the same thing, only it needs three coordinates for a point as it plots three-dimensional points. So to connect the point (1,2,3) to the point (5,7,8) we could use the command
>> plot3([1,5],[2,7],[3,8]); % connects the two points with a lineNotice, you may have your points given in terms of a vector, say v=á 1,2,3 ñ to plot these you can access the individual components as follows
>> v = [1,2,3]; plot3(v(1),v(2),v(3)); % plots the point associated to
% the vector v
The simple
m-files
qvector.m will allow you to plot
a vector with the command qvector(v)6.5.3 Plotting planes
To plot a line in two dimensions you make values of x and corresponding values of y and plot the pair of lists. For example this will plot a line>> m = 5; b = 2; % y = mx + b >> x = linspace(-5,10); % plot the line between -5 and 10 >> y = m*x+b;plot(x,y); % make the plotWe need to do exactly the same thing to plot a plane in MATLAB. So we need to generalize the linspace command and go from there.
Concept: equation of a plane
Recall the equation of a plane which is normal to the vector v, and goes through the point P=(x0,y0,z0) is given by
n · á x - x0, y - y0 , z - z0 ñ = 0
or solving, if n = á a,b,cñ then one has
a x + by + cz = d = n · (P) = ax0 + by0 + c z0.
if c is not 0 then we can solve to get z = (d - ax - by)/c.
So to plot a plane we first generate a mesh of values for x and y, then we find z and then we plot using the surf command. Here is an example
>> n = [1,2,3];p=[3,2,1]; % normal to n, through p >> [x,y] = meshgrid(-1:.1:1, -2,.1:1); % meshgrid like linspace. >> z = (dot(n,p) - n(1) * x - n(2) * y)/n(3); % n(3) non zero >> surf(x,y,z); % plots the surfaceThe m-files qplane.m will automate this for you, and plot the vector as well.
An important command for viewing planes is the view command. This allows you to change perspective.
>> view(n); % called with a vector. What is the
% output?
>> view([-3,0,1]); % a vector parallel to plane. Where did
% the plane go?
>> view([1,1,1]) % view from the point (1,1,1)
6.5.4 Plotting Cylinders
Concept: Plotting Cylinders
In Calculus, a cylinder is defined to be all the points which lie on lines that are parallel to a given vector, and go through a given curve. For example, the usual cylinder we think of is made up of all points on the lines parallel to the z-axis, or the vector k, that go through the curve given by x2+y2=1.
To plot a cylinder then we could simply shift the curve in the direction of our vector and then trace out the curve, repeating this several times. Here is an example
>> t = (0:25)*pi/25; % or linspace(0,pi,25)
>> x = t; y = sin(t); % parameterize the sine curve
>> z = zeros(size(x)); % make z a list of 0's, the same size
% as x
>> v=[-1,-2,3]; % our vector
>> plot3(x,y,z);
>> hold on;
>> for k=(0:10)/10 % loop between 0 and 1 10 times
plot3(x + k*v(1),y + k*v(2),z + k*v(3)); % plot the curve shifted
end
This is automated by the
m-files
qcylindr.m
(notice the silly spelling). (This is different than the built in
MATLAB command
cylinder
which plots a surface of revolution
despite its name.)To use the qcylinder command, we need to trace out a parameterized curve in the x,y-plane, and pick a vector. Here are some examples
>> t = linspace(0,2*pi);x = cos(t);y=sin(t); >> qcylindr(x,y,[0,0,1]) % parallel to z-axis >> qcylindr(x,y,[0,1,1]) % parallel to the vector [0,1,1] >> x = linspace(0,6*pi);y = sin(x); % a sine wave cylinder >> qcylindr(x,y,[0,1,1]) % parallel to the vector [0,1,1]
6.5.5 Plotting surfaces of revolution
Concept: Surfaces of revolution
Surfaces of revolution are surfaces associated with equations of the form
x2 + y2 = [f(z)]2
or any permutations of the three variables. The one above is a
surface of revolution about the z-axis. Notice for a fixed value
of z. the curve is a circle with radius |f(z)|.
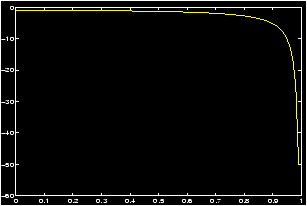
To plot a surface of revolution there is the MATLAB command cylinder. (A cylinder is a surface of revolution, as well as a mathematical cylinder.) If you don't like the language cylinder for a surface of revolution, you can use the m-files qsurfrev.m instead. Here are some examples, first Gabriel's horn (what is its volume? What is its surface area?)
>> z = linspace(1,100);r = (1)./z; % notice the dot >> cylinder(r); % or qsurfrev(r)Here is how a cylinder is a surface of revolution:
>> z = linspace(1:10); r = ones(size(z)); % all ones?? >> cylinder(r); % a cylinder!Here is cone:
>> z = linspace(1,10); m = 2; r = m*z; % cone with ``slope'' 2 >> cylinder(r); % or use qsurfrevHere is a sphere:
>> z = -1:.1:1; r = sqrt(1 - z.^2); % notice the dot >> cylinder(r); % or use qsurfrev
6.5.6 Plotting vector-valued functions
To plot a vector-valued function we need to associate a vector with a point. The point is the terminal point of the vector if its initial point is at the origin. Thus is the vector á 1,2,3 ñ then the point associated to this vector is the point (1,2,3). This is an easy concept to grasp, but is also very easy to get confused.A vector-valued function that we can plot should be a function of a single variable, returning a vector in 2 or 3 dimensions. For concreteness, we will consider functions of the type f(t) = á x(t),y(t),z(y)ñ. That is, the function returns a three-dimensional vector.
To plot, we simply associate the point with the vector, then this becomes the same problem as drawing a parameterized curve in three dimensions.
This will hopefully become clear with some examples:
Here is a helix: The function we are graphing is f(t) = á cos(t), sin(t),tñ.
>> t = linspace(0,4*pi); >> x = cos(t);y=sin(t);z=t; >> plot3(x,y,z); % plots the parameterized curveHere is a straight line given by a point and a vector:
>> p = [1,2,3]; v = [0,1,3]; % a point and a vector
>> t = linspace(-3,3);
>> x = p(1) + t*v(1); y = p(2) + t*v(2); z = p(3) + t*v(3);
>> plot3(x,y,z); % plots the line. Use view to get
% different views
Here is the flight of a baseball to right center
>> t = linspace(0,5); >> x = 100 * cos(pi/4) * cos(pi/6) t; >> y = 100 * cos(pi/4) * sin(pi/6)*t; >> z = 3 + 100 * sin(pi/4) * t - 16 * t.^2; % notice the dot >> plot3(x,y,z);
6.5.7 Plotting functions z=f(x,y)
The plot of a function z = f(x,y) is done by plotting the triples of points (x,y,f(x,y)), just as the plot of the function y=f(x) is the plot of the pairs of points (x,f(x)). To do such a plot, we need to define the values of x and y which is done with meshgrid and then find the corresponding z values. This exactly what we needed to do to plot and plane, and the idea is no different. Here are some examples.Here is the plot of the bell curve
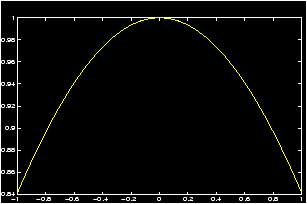
>> temp = -3:.1:3;[x,y]=meshgrid(temp,temp); >> z = (1/sqrt(2*pi)) * exp((x.^2+y.^2)/2); % the bell curve >> surf(x,y,z); % use the surf commandPlot the egg carton f(x,y) = sin(x) * sin(y):
>> temp = -3*pi:.1:3*pi;[x,y]=meshgrid(temp,temp); >> z = sin(x) .* sin(y); % notice the ``dot'' >> surf(x,y,z)Plot the function f(x,y) = cos((x2 + 2y2)/4)
>> temp = -pi:.1:pi; [x,y]=meshgrid(temp,temp); >> z = cos((x.^2 + 2*y.^2)/4); >> surf(x,y,z);
6.5.8 Plotting with csimovie.m
You can use the function csimovie top plot 3d trajectories. Try the help command to find out more information. The file csimovie.m is installed on the CSI network, or can be found here for you to install.7 Finding zeroes
In this section we learn several methods for finding zeroes of a function. A brief note on vocabulary is in order.- If we have an equation, we talk about solutions to the
equation: For example the equation sin x = cos x has solutions
in [0,2p] given by x = p/4 and x=5p/4.
- If we have a function f(x) then a zero of f(x) is a
value x for which f(x) = 0. To relate to a solution, let f(x) =
sin x -cos x. Then the zeroes of f(x) are the
solutions to the equation sin x = cos x
- If we have a polynomial f(x) then the zeroes often get a special name: roots. So, if f(x) = x2 + 5x + 6 then the roots of f(x), (x=-3 or x=-2) are the solutions to f(x) = 0.
7.1 Graphically finding zeroes
Here is an example to illustrate how we can find zeroes of a function using the graphing capabilities of MATLAB.Example: Finding zeroes graphically
Find all solutions of the equation x3 = 20 cos x.
(Notice that this is a non-linear problem, and can't be solved by tricky algebra.)
We have two choices to solve for the solutions graphically. We could plot both the function x3 and the function 20 cos x on the same graph, and then look for points of intersection, or we can take the difference of the two sides, and looks for zeroes of the function f(x) = x3-20cos x. We'll do the latter.
- Let f(x)=x3-20cos x and determine all x values that
satisfy the equation f(x)=0. These x values are called the
zeros of f or solutions of the equation f(x)=0.
- Create a graph of y=f(x) over a wide domain say from -2p
to +2p so that the approximate locations of the roots may be
observed.
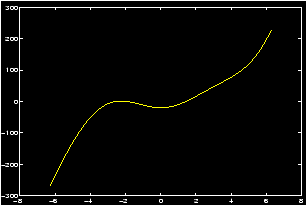
>> x=-2*pi:.01:2*pi; y=x.^3-20*cos(x); plot(x,y), grid
- Examine the resulting graph closely. Since the function 20
cos x is bounded by 20, and |x3| > 20 if x>3, It is evident
from the graph that all the solutions are located in the
interval [-3,2]. To read their locations more accurately, we
create a new plot covering only this interval. Thus changing the
range of x accordingly, we enter:
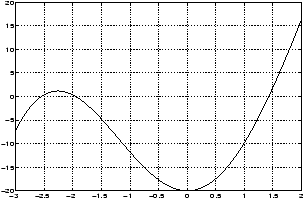
>> x=linspace(-3,2); >> y=x.^3-20*cos(x); % redefine y to match new x! >> plot(x,y), grid
- From this graph we see that nonzero positive solutions are
located in the intervals [-2.5,-2], [-2,-1.5] and [1,1.5]. Let us
concentrate on the root in [1,1.5]. To read its location more
accurately, we create a new plot covering only this interval. Thus
changing the range of x we enter:
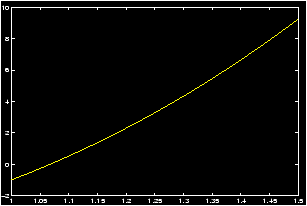
>> x=1:.001:1.5; y=x.^3-20*cos(x); plot(x,y), grid
We can now see that the root falls within the interval [1.4,1.5]. We could continue in this fashion and determine the root even more accurately. However, we wish to introduce a new feature of MATLAB which could speed up the determination of the root by zoom ing in and enlarging just the area near the point where the root is located. So, on the command line type:>> zoom on
Use the mouse to move the arrow around and point to where the root is located, and click with the left mouse button. The area is enlarged and you can see that the root is slightly greater than 1.42. Repeat this process of pointing to the root and clicking with the left mouse button. After a few repetitions you could approximate the root by x» 1.4255.
How good is this answer? If it is very close to the zero, the value of the function at 1.4255 must be very close to zero. Verify this by entering:>> x=1.4255; y=x.^3-20*cos(x)
which results iny = 9.7482e-004
It may not appear to be so, but the -004 says this is 0.00097482 which is indeed very close to zero. (You should not expect to get exactly 0 for an answer, as the solution is most likely irrational, and your answer will only be an approximation of the true zero.
When you no longer need the zoom feature, you should turn it off by typing>> zoom off
7.2 Finding roots of polynomials
Finding zeroes of a polynomial is made easy by the built-in MATLAB command roots .Example: Finding roots of polynomial
Consider the polynomial f(x)=2x3+6x2-4x-5. To find the roots (or zeroes) of f(x) we graph the function on the interval [-4,3].
>> x=-4:.001:3; y=2*x.^3+6*x.^2-4*x-5; >> plot(x,y), grid
There are three real zeros on the intervals [-4,-3], [-1,0] and [1,2]. The values of these roots can be obtained by zooming graphically as was done in this example.
However, for polynomials, MATLAB has a special built-in function roots which can find these roots directly. To use this function one needs first to specify the polynomial in terms of the coefficients of the powers of x.
Example: Example of representing a polynomial with a vector
The polynomial in this example is represented by
p=[2 6 -4 -5].
Note that in the array the coefficients are listed in the
order of descending powers of x starting with the coefficient of
the highest power. (If a particular power of x is not present in
the polynomial, then its coefficient is listed as 0. Thus, for
example, the polynomial 5x3+2 would be represented by
p=[5 0 0 2].) In general, this way of thinking may be of
help: Think of the coefficients of the polynomial as
c(1) xn + x(2) xn-1 + ···+ c(n-1) x2 + c(n) x + c(n+1)
then your polynomial is represented by c.This may be familiar from the ``synthetic division'' technique for finding the value of a polynomial evaluated at c, or dividing f(x) by x-c.
The following sequence of MATLAB commands determine the roots of f(x):
>> p=[2 6 -4 -5]; % place a space or a comma between coefficients >> r=roots(p) % or simply roots([2,6,-4,-5])which yields the roots:
>> r ans -3.3732 -0.6943 1.0675 % actually a column vector
Concept: Some Theory about Roots of Polynomials
Most math students know that the roots of a 2nd degree polynomial or quadratic polynomial can be found with the quadratic equation . That is if f(x)=ax2+bx+c then the solutions to f(x) = 0 are given by
(-b ± b2 - 4 ac)/2a.
When the discriminant
(b2 - 4 ac) is negative then there
are 2 complex-valued solutions (which are conjugate) and no real
solutions (the graph of f(x) does not intersect the x-axis) when the
discriminant is 0 there is 1 solution which is a multiple root, and
when the discriminant is positive there are two distinct
roots. Counting multiplicity then we have the fact that a quadratic
polynomial alway has 2 roots.There are two ways to go from here. First, you may be surprised to know that there are formulas that will give the roots of a third- or a fourth-degree polynomial. However, there is no formula that will work for all fifth- of higher-degree polynomials. (A major feat of mathematics proven in the early 1800's after centuries of effort.)
Secondly, and what is important here, is the Fundamental Theorem of Algebra which states that a polynomial of nth degree will have n roots when we count multiplicities and complex-valued roots.
So when we use the roots command of MATLAB with a nth degree polynomial we have the following: the nth degree polynomial is entered in as a row vector with n+1 elements, and the answer is a column vector with n elements.
You may ask, how does MATLAB find its roots for a polynomial with degree 5 or higher if there is no possible formula. The answer lies in finding good approximations. Newton's method is an old method to find such approximations.
7.3 Newton's method
Newton's method is an algorithm to find numeric solutions to the equation f(x) = 0. We have already seen other methods to do this, namely the commands roots for polynomial functions, and the graphical solution .The general idea idea of Newton's method is easy to understand. Consider the graph of the function f(x) = x3 - 3.
By looking at a graph, we see that there is a solution to the equation f(x) = 0 in the interval [0,5]. Call this solution c. Newton's method will help us find a numeric approximation to this value of c. The zig-zagging lines are a graphical representation of the method. Notice how they converge to the desired value of c. These lines were generated as follows. We start at some initial point x0 (in the picture x0=5). It should be a reasonable approximation to c. Once we have x0 we draw a vertical line until we intersect the graph of f(x). Then we follow the tangent line to f until it intersects the x-axis. We use the tangent line because we know it approximates the function quite well near the point (x0,f(x0)). This point of intersection is our new guess x1. This is about 3.3 for the graph. We then repeat, or iterate, this process to find a sequence of points x2, x3, and so on. We stop when the new values of xn don't change too much, or when f(xn) gets very close to 0.
Given the point xn, the next point xn+1 is found by calculating the point at which the tangent line to the graph of f(x) at (xn,f(xn)) intersects the x-axis. We know a point, and the slope of this line (it is f'(xn)) and so this is easy to do. The tangent line in point-slope form has the equation
y - f(xn) = f'(xn) ( x - xn)
Solving for the x-intercept gives xn+1:
xn+1 = xn - f(xn)/f'(xn).
In MATLAB the subscripts are not used as the equals sign is assignment and not equality. (Consider the difference between x = x+1 and x = x+1.) Thus to apply Newton's method with an initial guess of x0 = 5 we would simply type
>> format short >> x = 5 % our initial guess >> x = x - (x^3 - 3)./(3*x^2) % the left x is x_1 the right one x_0 x = 3.3733 % x_1 >> x = x - (x^3 - 3)./(3*x^2) % the left x is x_2 the right one x_1 x = 2.3368 % x_2 >> x = x - (x^3 - 3)./(3*x^2) % the left x is x_3 the right one x_2 x = 1.7410 % x_3 ..... % repeat a few steps >> x = x - (x^3 - 3)./(3*x^2) % the left x is x_5 the right one x_6 x = 1.4423 % x_6 >> x = x - (x^3 - 3)./(3*x^2) % the left x is x_7 the right one x_6 x = 1.4422 % x_7 >> x = x - (x^3 - 3)./(3*x^2) % the left x is x_8 the right one x_7 x = 1.4422 % x_8And we see that the solution has converged to 1.4422. Checking that this is a root we evaluate
>> x^3 -3 ans = 0
- Newton's Method can be automated quite easily. An example m-file can be found here: newton.m. To use this, you must first have created m-files for f(x) and f'(x).
- Newton's Method has a few cases where it works quite badly. You
may be interested to see why: Here are some examples:
Example: Too close to a minimum.
Graphically explore the root that Newton's method finds whenf(x) = x3 + 2 x2 - 30 x -5.Compare the graphical output of Newton's method with the following initial points: x0 = 2,2.20,2,35,2,45. You should see that as the initial guess gets closer to a point on the graph with a 0 derivative, that the method takes much longer to converge.
Example: Cycling.
Let f(x) = x3 - 5x. Factor f(x) exactly to find its roots.
Now use Newton's method with an initial guess of x0=1. What happens to the subsequent iterations? Can you see what is happening from the graph?
Now try an initial guess of x0=2. Does the same problem occur?
Example: Divergence.
Let f(x) = x1/3. Clearly x=0 is the only root. By hand (it is easier) compute and simplify f(x)/f'(x). From this compute the sequence of points obtained by Newton's method starting from x0=1. Is it getting closer to 0?
- Here is a challenging problem where Newton's method can yield
the answer.
Example: Medical Dosage
A drug administered to a patient produces a concentration in the blood stream that can be modeled byC(t) = Nt e- 0.2 twhere N is the initial dosage injected in milligrams (mg) and t is the time in hours since the injection. Suppose it is known that the maximum safe concentration of this drug in the blood stream is 2 mg/ml.- When does the maximum concentration occur? Note that the value of N does not affect this answer.
- What amount N should be injected so that the maximum concentration is 2 mg/ml? N need not be an integer.
- With N from above, suppose that an additional amount of this drug is to be administered to the patient after the concentration falls to 0.25 mg/ml. Determine, to the nearest minute, when this second injection should be given.
- Assuming that the concentration from consecutive injections is additive, and assuming that the second injection uses the same amount N of the drug as in the first injection, what will the maximum concentration in the blood stream be after the second injection? Should N be adjusted to ensure that the maximum concentration is still safe?
8 Limits
Concept: Definition of a limit.
The notion of a limit of a function was originally introduced in order to make the definition of derivative make sense. However, it can also be used to describe the behavior of a function near a given point, as well as to find and describe asymptote s.
One needs to compute limits of the form limx ® a f(x) to compute the slope of a tangent line or the derivative of a function, as well as to determine whether a function is continuous.
The definition of a limit of a function, which can be found in any calculus textbook, forms the basis for both a graphical and numerical approach to finding limits.
To summarize it in a means suitable for MATLAB exploration, one has as the value of x gets close to a desired number (often called c), then the value of f(x) gets close to a number L called the limit.
If we want to check out a limit with MATLAB we need to understand this graphically and numerically. Graphically it says if we follow the graph of f(x) towards c from the left or the right, the corresponding y values converge to a limit. Numerically, this says if we look at the sequence of y values corresponding to any sequence of x values which gets close to c then the y values should get very close to a single number -- the limit.
A key result we'll need is that limx ® a f(x) = L if and only if both limx ® a- f(x) = L and limx ® a+ f(x) = L. In other words, we have the following.
The two-sided limit exists if and only if the left- and right-sided limits both exist and are equal.
Thus, to show that the limit is L, essentially we need to show that, as x takes values closer to a (on both sides of a), f(x) takes values closer to L.
-
Example: Finding Limits Graphically
Let us use a graphical approach to determine limx ® 0 sin x/x.
Notice this function is not defined at x=0, and ``plugging in'' x=0 gives an indeterminate form of 0/0. Thus the limit takes work to figure out. However, this function is defined for all x except at x=0, which is all that is required to apply the limit definition. The following MATLAB commands will plot the graph of sin x / x near x=0.
>> x=linspace(-1,1); % plot for x in the interval [-1, 1] >> y=sin(x)./x; % `dot' makes division point wise >> plot(x,y), grid
From the graph you notice as one moves toward 0 from either side on the x-axis, the y values move toward 1. From the graph you can tell what the limit is 1.
-
Example: Finding Limits Numerically
Here is a simple method for finding the same limit numerically.
>> format long % gives extra decimal places >> x=[-.1 -.01 -.001 -.0001 -.00001] % x approaches 0 from the left >> y=sin(x)./x; [x;y]' % print x,y in a 2-column table >> x=[.1 .01 .001 .0001 .00001] % x approaches 0 from the right >> y=sin(x)./x; [x:y]'
You should get the following results (x on the left, sin (x)/x on the right):ans= -0.10000000000000 0.99833416646828 -0.01000000000000 0.99998333341667 -0.00100000000000 0.99999983333334 -0.00010000000000 0.99999999833333 -0.00001000000000 0.99999999998333 ans= 0.10000000000000 0.99833416646828 0.01000000000000 0.99998333341667 0.00100000000000 0.99999983333334 0.00010000000000 0.99999999833333 0.00001000000000 0.99999999998333Since the values in the right columns both approach 1, we conclude that both right and left limits are 1 and so the limit is 1 as well.
-
Example: limit of slope of the secant line:
See the secant line example to find the definition of the secant line. Essentially we have a function f(x) a point x1 and a point x2. Let x2 = x1 + h. So that h measures the difference between the two values of x. Then as h gets close to 0 x2 and x1 get close to each other. If the limit as h goes to zero exists then the function is said to have a derivative at x1.
In the secant line example we see how to plot the function sin(x) and the secant line between x1 = p/4 and x2 = x1 + h with h = p/8. By changing the value of h we see it is a simple matter to find graphically the limit of the secant lines.
To find the slope numerically we recall the definition of the slope of a linem = (f(x1+h) - f(x1))/(x1 + h - x1) = (f(x1+h) - f(x1))/ hSo in MATLAB we define a sequence of values h converging to 0, and then plug into the formula:>> x_1=pi/4; n = 1:5; h = 10.^(-n); % suppress the output with ; >> m = ( sin(x_1 + h) - sin(x_1)) ./ h; % we need the ./ as h is a % list >> [h;m]' % print out in columnsIf you repeat this using -h in the second and 3rd line you will see that the left and right limits are the same and equal 0.70710 (=2/2).
9 Derivatives
9.1 Difference quotients
Concept: Definition of a derivative
Let f(x) be a function defined in a neighborhood of the point x=x0. The derivative of f(x) at x=x0 is defined by the limit
| f | (x0)= |
|
(f(x)-f(x0))/(x-x0), |
Since x is close to x0 during the limit process described above, it is convenient to let x=x0+h and think of h as being small and approaching to zero. Note that h can be positive or negative corresponding to the approach from the right or from the left, respectively. Thus we have the definitions (you may be reminded of the secant line example )
difquo = (f(x0+h)-f(x0))/h
and
| f | (x0)= |
|
(f(x0+h)-f(x0))/h. |
Therefore, given a small value of h, difquo, as defined above, is an approximation of the derivative of f(x) at x0. The smaller the value of h is, the better the approximation. Furthermore, since x0 can be any point in the domain of f(x), we write
| dy/dx = f | (x)= |
|
(f(x+h)-f(x))/h |
So, to find the approximate derivative of a differentiable function f(x) over an interval, we may use the difquo function which is
difquo(x)= (f(x+h)-f(x)) /h,
using a small value of h such as h=0.1 or 0.01.Example: Graphing the difference quotient:
Let us create a plot of the derivative of f(x)=cos x over the interval [0,2p] based on the numerical evaluation of its difference quotient. We shall use h=0.01 in evaluating the difference quotient. The following MATLAB commands will plot both the function and its approximate derivative together.
>> h=0.01;
>> x=0:0.001:2*pi; % step size should be smaller
% than h
>> difquo=(cos(x+h)-cos(x))./h; % difference quotient
>> plot(x,cos(x),'r',x,difquo,'b'),grid % plot cos in red and difquo in blue
>> axis([0 2*pi -1 1]) % a better frame for the
% graph
Here is another example which shows that we can reduce typing quite a bit, and hence possible errors.
Example: Baseball with wind correction
If there is constant acceleration, a baseball thrown from a height of x0 feet with an initial upward velocity of v0 feet/sec will fall according to the formula (0 £ t £ T).
y(t) = x0 + v0 t - 16 t2.
Here T is the time that the ball hits the ground.If we assume a slightly more realistic model, then the acceleration will depend upon the velocity of the baseball. A model for this yields the new formula for 0 £ t £ T.
| w(t) = x0 - 16 t + | ( | (16 + v0)/2 | ) | ( | 1 - e-2t | ) | . |
Let's suppose we want to follow the path of a baseball thrown from a fourth story window during the Yankees World Series Championship parade. Let x0 = 48, and v0 = 32.
-
Plot both functions y(t) and w(t) so that you can
determine from the graph the respective values of T.
To find an estimate on the domain to plot the the two functions we note that the baseball under y(t) will hit the ground when the polynomial y = -16 t2 + 32 t + 48.>> roots([-16 32 48]) % find the zeroes ans = 3, -1 % actually a column vector
So T=3 for y(t) when the ball hits the ground. We expect the ball with wind-resistance to fall more slowly, so let's plot the functions over the interval [0,5].
>> t = linspace(0,5); x0=48;v0=32; >> y = -16*t.^2 + v0*t + x0; % remember the .^ >> w = x0 - 16*t + (16+v0)/2 * ( 1 - exp(-2*t)); >> plot(t,y,t,w); >> T = 4.5; % an approximation
We see that 4.5 is about correct for T for w(t).
Now answer questions about the ball with wind-resistance.
- What is the average velocity of the baseball
during [0,T].
This is given by (w(T) - w(0))/T. To compute this without typing too much, let's use the up-arrow keys to give w. Notice w is defined for t = linspace(0,5) but we'll just redefine it to be T.>> t = 0; >> w0 = x0 - 16*t + (16+v0)/2 * ( 1 - exp(-2*t)); % use up arrow key, % and edit >> t = T; >> wT = x0 - 16*t + (16+v0)/2 * ( 1 - exp(-2*t)); % use up arrow key % and edit >> avg = (wT - w0)/T % pretty easy if done smartly - Let h= 0.1, plot the difference quotient of w(t) over the
interval [0,T].
We want to again use our definition of w(t) to minimize typing. Notice, we need to add an h in the right place.>> t = linspace(0,T); h = 0.1; >> w = x0 - 16*t + (16+v0)/2 * ( 1 - exp(-2*t)); % from up arrow >> wh = x0 - 16*(t+h) + (16+v0)/2 * ( 1 - exp(-2*(t+h))); % from up % arrow. >> difquo = (wh - w)/h; >> plot(t,difquo) - What is the time t when the ball is at
its highest point? What is the height?
Using Calculus, we know this is when the derivative is 0, from the graph of the difference quotient this is t=1.
- The difference quotient is a good approximation to the
instantaneous velocity. From the graph, find the instantaneous
velocity when the ball hits the ground?
We see from the graph that it has a horizontal asymptote of -16. This says that the velocity stops decreasing after a certain amount. This is called a terminal velocity. From the graph it appears that T is big enough so that the ball is very near the terminal velocity, so we'll say the instantaneous velocity is -16 when the ball strikes the ground/
Concept: Implicit differentiation
Sometimes you are confronted with finding rates of change but you don't have a function relating x and y but rather an equation. That is y is implicitly defined in terms of x. The trick in mathematics is to take d/dx of both sides, use the chain rule properly and then solve for dy/dx in terms of x and y.
Using MATLAB to find numeric estimates requires a slightly different tack. Here is the main idea.
- Turn you equation into a problem involving level curves of a function: F(x,y) = c for some constant c.
- Differentiate using the chain rule:
Then solve to get
d dx F(x,y) = (Fx(x,y),Fy(x,y)) · (1, dy dx ) = 0 where Fx is the partial derivative in the x variable. We can use MATLAB to find this just as before because partial derivatives are just like regular derivatives of a function of a single variable.dy dx = - Fx(x,y) Fy(x,y)
|
(x2 - y6) = 2x - 6y5 |
|
= |
|
1 = 0 |
|
= |
|
Using the difference quotient to estimate Fx and Fy we get instead the following. Suppose F(x,y) = x2 - 6y5 is defined in an m-file.
>> y0 = (1 - 1/4)^(1/6) y0 = 0.95318 >> x0 = 1/2 x0 = 0.50000 >> h = .01 h = 0.010000 >> -(F(x0+h,y0) - F(x0,y0)) / (F(x0,y0+h) - F(x0,y0)) ans = -0.20839 % this is the approximate value >> (-2*x0)/(6*y0^5) ans = -0.21182 % this is the exact answerThe answer is not too far off and could be improved by using a smaller value of h. Notice that we used the secant line approximation for Fx and Fy
| Fx(x,y) » |
|
, Fy(x,y) » |
|
9.2 Symbolic derivatives
10 Integration
10.1 Riemann Sum
MATLAB has a command rsums that allows you to graphically explore Riemann sums. Here is an example.Example: Find ò01 e-3x dx.
>> rsums exp(-3*x)MATLAB has given you a window (you may have to click on windows and then on figure no. 1) which shows the Riemann sums for exp(-3*x) on the interval [0,1] when n=10. To increase n, click on the right arrow at the bottom. The value of the Riemann sum is shown above the graph. You can watch this value change as you increase n.
Compare this answer to
>> numeric(int('exp(-3*x)',0,1))
Notice: With the command
rsums
you can only use the
interval [0,1] and you can only use the maximum n allowed by this
graph.10.2 Simpson's Rule and other numerical methods
10.3 Symbolic integration
MATLAB has a built in ability to compute symbolic integrals. You will need to be familiar with the symbolic math operations to fully appreciate this.Note: MATLAB has improved and different symbolic math capabilities in version 5.0 and greater. These notes refer to earlier versions.
- Finding Antiderivatives
Example: Use MATLAB to compute ò e-3xdx. Answer: Of course you know how to find this easy antiderivative by hand. But we'll use it to illustrate how to find integrals using MATLAB.>>int('exp(-3*x)') ans= -1/3 * exp (-3*x)We know the answer should be -(1/3)e-3x +C, with a ``constant of integration" C. MATLAB omits this constant, but that doesn't mean you should!
- finding a second derivative
Example: consider>>int ans= 1/9*exp (-3*x)
MATLAB has found the antiderivative of the last answer namely the antiderivative of -1/3 * exp (-3*x).
one can use the diff command to recover the integrand:>> diff
- Finding definite integrals
MATLAB can compute definite integrals as well.
Example:>>int ('exp (-3*x)', 0, 1) ans = -1/3 * exp (-3)+1/3This computed the following ò01 e-3x dx.
- numeric answers
What if you wanted a number? You can use the
numeric
command:
>> numeric % for the last integral done above ans = .3167
- Simplifying messy integration
Often the answer MATLAB gives is quite hard to read. It has a built
in simplify command to help in these cases:
>> int('sin(x)^7 * cos(x)^5') ans = TOO UGLY TO PRINTTo see how MATLAB simplifies this answer, use the simplify command and then the pretty command:>> simplify % simplifies the last integral >> pretty % makes it _pretty_
Do this example with MATLAB. Is it ``prettier''?
- When there is no antiderivative
Sometimes there is just no antiderivative for a given function. So
the
Fundamental Theorem of Calculus
will offer no
help in finding an answer to a definite integral. You need to
approximate the answer if you want to move on. Again we use
the MATLAB command
numeric
. As well, you could approximate
the integral with a
Riemann sum
, or use
Simpson's Method
.
>> int('\cos(x^3)', 0,1) % if MATLAB chokes it prints out its input ans = int('\cos(x^3)', 0,1) >> numeric % find numeric answer to last query ans = 0.9317
10.4 Multiple integration
11 Sequences and Series
11.1 Sequences
11.1.1 Defining a sequence a = {an}
In MATLAB there is a natural way to describe a sequence in terms of a list. Recall the sequence {an} is nothing more than a list of numbers indexed by n. But a vector in MATLAB is just the same.>> a = 1:100; % the sequence 1,2, ..., 100 >> b = 1:2:100; % the odd numbers between 1 and 100 >> for i = 1:10 > c(i) = prod(1:i); % shorthand for the factorial of i >> end % c is the sequence 1!, 2!, 3!,... 10! >> x = floor(2*rand(1,100)) % a sequence of 100 random coin tosses
11.1.2 Sequence found by iteration: an = f(an-1)
11.2 Series
12 Appendix
12.1 Mathematics terminology
- dot product
: The dot product or scalar product between
two vectors is formed by matching up corresponding coordinates,
multiplying then adding. For example
(1,2,3) · (4,5,6) = 1(4) + 2(5) + 3(6) = 32.In MATLAB this could be done with the following commands:
>> a = [1,2,3]; b = [4,5,6]; % define two vectors >> dot(a,b) % returns 32
Which uses the dot command. Alternatively we could have used matrix multiplication>> a * b' % using matrix multiplication
- cross product
: The cross product between two
three-dimensional vectors u and v is a vector with
direction given by the right-hand rule and magnitude given by
||u||||v||sinq. In MATLAB it is found with the
cross
command
>> u = [1,2,3]; v = [4,5,6]; % two vectors >> w = cross(u,v) % the cross product ans = -3 6 -3 >> dot(u,w) % cross product is orthogonal to u and v ans = 0
- scalar
: In Linear Algebra, a scalar is a name for a real
number.
- matrices
and a matrix
: In Linear Algebra a
matrix is a n × m tabular array of numbers with n rows and
m columns. Matrices are quite useful for things such as keeping
track of systems of equations, keeping track of connections between
nodes on a graph, or even representing operations of a robot arm
such as rotations. In MATLAB we can enter a matrix quite easily. For
example this enters in a 2 by 3 matrix
>> [1, 2, 3; 4, 5, 6] % the matrix [1 2 3] % [4 5 6] - matrix multiplication
: In Linear Algebra the product
between two matrices A and B are defined if A is n by m
and B is m by p. Notationally it is given by
MATLAB uses the usual multiplication symbol
(AB)i,j = n å k=1 Ai,k Bk,j. *for matrix multiplication when the two quantities are matrices.>> A = [1,2;3,4] % A is 2 by 2 >> B = [5,6,7;8,9,10] % B is 2 by 3 >> A*B % answer is 2 by 3 ans= 21 24 27 47 54 61 >> B*A Warning, Warning Will Rogers % Who said you could do this! Wrong sizes
- transpose
: in Linear Algebra the transpose operator
changes a n by m matrix into an m by n matrix by switching
the indices. In MATLAB it is indicated with the ' sign. A
typical example is to transform a row
vector
into a column
vector.
>> v = [1,2,3] % a row vector >> v' % a column vector
- vector
or list
: In Linear Algebra a vector is a list of
numbers of a certain size. It can be a row vector such as
>> [1, 2, 3] % the vector (1,2,3)
or a column vector, which in MATLAB is entered in with>> [1;2;3] % the vector (1) % (2) % (3)In Physics, a vector is a mathematical quantity that represents a magnitude and a direction. A vector becomes a list of numbers once we chose a coordinate system, and identify a vector with the directed line segment from the origin to a point. Often the distinction between a column vector and a row vector is not made, but it is important to MATLAB.
12.2 Calculus terms
Here are some familiar terms from Calculus:-
continuity
. Contiuity of a function
is the property that the function has a limit, and the limit has the
proper value. The limit as x goes to c exists and is f(c). A
discontinuous function
is one where
either the limit does not exist (for example sin(1/x) at x=0)
or when the limit does not have the correct value.
- plane
. A plane is made up of all solutions to a linear
equation in 3 unknowns. The general form of a plane is
a x + b y + c z = d.This plane is normal to the vector á a,b,c ñ.
- Vector-valued functions
. A
function whose range is a subset of Rn, n>1.
- Asymptotes
. An asymptote is a way of
describing how a graph looks when an infinity is approached. A
horizontal asymptote for example tells us the behaviour of a
function as x = -¥,a nd x = ¥ are approached.
- Sequences
. Technically, a sequence is just a
funciton whose domain is a subset of the integers, usuall the
positive integers. An example is the harmonic sequence 1,1/2,1/3,....
- Domain of a function . The domain of a function consists of all values for which the function is defined.
12.3 Some internet miscellania
Here are some definitions of some terms found in this tutorial and on the internet:- LaTeX
: LATEXis the standard typesetting program for
mathematicians throughout the world. It was used to make this
manual. If you are curious, and a bit adventuresome, you can find
out more at
http://www.tug.org
- UNIX
: UNIX is an older and much more mature operating
system that Windows 95 or Windows NT. To find out more, you may be
interested in a free implementation for personal computers, called
linux
. For more information see
http://www.redhat.com.
- emacs
: Emacs is an editor/kitchen sink prevalent in the
UNIX
world. There are versions available for Windows 95,
Windows NT and Windows *. For information, you can try the XEmacs
home page at
http://www.xemacs.org.
- linux
: a free implementation of the
UNIX
operating system for personal computers. (As well, powerPC
MacIntosh's and some workstations.) For more information you can try
http://www.redhat.com.
- postscript
: Postscript if a computer language that
controls many printers. Consequently it is the default way to share
files among internet users. In order to view or print postscript you
need an interpreter (if you are a windows user). You can find one at
http://www.cs.wisc.edu/ ghost/aladdin/
- m-files
: An ``m-file'' in MATLAB is a way to store
functions for later use. MATLAB stores functions in files which have
the file extension .m, for example test.m,
factorial.m, etc. An ``m-file'' needs to have a special
syntax. You can read more in the section on
m-files
.
- script files : a script file in MATLAB is a way to store several key strokes for later use. In contrast to an m-files , you can not pass arguments to a script file. Script files should have the file extension .m.
13 Adding to this tutorial
If you are interested in adding to this tutorial you are more than welcome. It would be great to have more topics, more examples, more problems and better written descriptions.Here's what you can do:
- You can make a comment or question available on the web by
posting to the MATLAB hypernews
forum.
- If you would like to make a comment about something in the tutorial please send e-mail to verzani@postbox.csi.cuny.edu . Feel free to discuss how topics are presented especially if they are not clear or thorough enough.
- If you would like to write a new section, you should have some familiarity with LaTeX , as these pages are created with tth a latex to html converter. There are a few special macros which are available to make the conversion to hypertext fairly trivial. For more info send e-mail to verzani@postbox.csi.cuny.edu .
14 Credits
This tutorial was prepared by John Verzani. Most of the material was copied verbatim for the projects for math 229, 232 and 233 that were created by the faculty of the Department of Math. Kim Vuu had a hand in the creating of many of the figures contained herein.Valuable comments were provided by Marcelo Coca-Perraillon on implicit differentiation.
This list is buggy.
Index
|
|
This document was translated from LATEX by HEVEA.